Phathoc.net - Chinese - 鈕衛星： “時食”與“非時食”的判定 ------—

Phật Học Online

鈕衛星： “時食”與“非時食”的判定 ------——天文學為佛教戒律提供技術支援之一例

作者：鈕衛星

“非時食”戒是佛教最基本的戒律之一，目的就是為了約束僧眾每一天都在規定的時間內進食。許多佛典，尤其是律部經典中，對此規定都有記載。例如，據《阿毗達磨俱舍論》卷十四載：“何等名為八所應離？一者殺生，二不與取，三非梵行，四虛誑語，五飲諸酒，六涂飾香鬘、舞歌觀聽，七眠坐高廣嚴麗床座，八食非時食。”[1] 這就是通常所謂的八戒，“非時食”被列為八大戒律之一種。也有把“涂飾香鬘”和“舞歌觀聽”分列為二戒的，這樣總有九戒，前八者為戒，后一者為齋法，統稱為“八戒齋”，這是在家修行的居士所應持有的基本戒律。又據《沙彌十戒法並威儀》載，初出家沙彌所持十戒為：不殺生、不盜、不淫、不妄語、不飲酒、不著香華鬘不香涂身、不歌舞倡妓不往觀聽、不坐高廣大床、不非時食、不捉持生像金銀寶物。[2]“非時食”戒也被列為初出家的沙彌所應持有的基本戒律之一。

然而，在沒有鐘錶的原始佛教時期，為何要制定出這樣一條戒律出來？當時的佛徒又如何在技術上判斷“時”與“非時”以確保此一戒律得到嚴格遵守呢？本文欲就這些問題進行一番探討。

一、過午不食的來曆：“非時食”戒的起源和實施情況

佛教戒律中，並不是一開始就有“非時食”戒這一條的。據《彌沙塞部和醯五分律》卷八“初分墮法”載：

佛在王舍城，爾時未為比丘制非時食，諸比丘于暝夜乞食，或墮溝塹，或觸女人，或遇賊剝，或為蟲獸之所傷害。食無時節，廢修梵行。時迦留陀夷著雜色衣，面黑眼赤，闇中乞食。有一懷妊婦人，電光中見，便大驚喚言：“毗舍遮[1]！毗舍遮！”迦留陀夷言：“我是沙門乞食，非毗舍遮。”便苦罵言：“汝何以不以刀決腹，而于暝夜闇中乞食？余沙門、婆羅門一食便足，汝今云何食無晝夜？”諸長老、比丘聞，種種呵責，以是白佛。佛以是事集比丘僧，問迦留陀夷：“汝實爾不？”答言：“實爾，世尊。”佛種種呵責已，告諸比丘：“今為諸比丘結戒，從今是戒應如是說，若比丘非時食，波逸提。[2]”爾時有比丘服吐下藥，不及時食，腹中空悶。諸比丘不知云何，以是白佛。佛言以酥涂身，猶故不差；佛言以糗涂身，猶故不差；佛言酥和糗涂身，猶故不差；佛言以暖湯澡洗，猶故不差；佛言與暖湯飲，猶故不差；佛言以盆盛肥肉汁坐著中。以如此等，足以至曉。一切不得過時食。非時者，從正中以后至明相[3]未出，名為非時。若比丘非時、非時想、非時疑、非時時想，皆波逸提。時非時想、時疑，突吉羅。[4]比丘尼亦如是。[3]

佛教徒的食物皆靠居士供給，起初佛祖沒有規定進食的時間，以致出現了上引經文中的種種問題，不利於修行。於是佛祖規定“正中”以后、天亮以前不能進食。所謂“正中”就是太陽在正南方的時刻，用天文學術語來說就是太陽上中天經過子午線那一瞬間。所以“非時食”戒也常常叫做“過中不食”或“過午不食”。自從佛祖定下上述規矩之后，“非時食”戒便成了佛教最基本的戒律之一，本文開頭提到在佛教的“在家八戒”和“出家十戒”中都列入了這一戒條。

“非時食”戒成為如此重要的一條戒律，出家僧侶自然必須嚴格遵守，就是一般信仰佛教的俗家人士也常以此戒律自守。梁武帝就是一個著名的例子。梁武帝崇信佛法，雖貴為帝王，也遵守“過中不食”的戒條。據《梁書·武帝本紀》載：“（帝）日止一食，膳無鮮腴，惟豆羹糲飯而已。庶事繁擁，日倘移中，便嗽口以過。身衣布衣，木綿帛帳，一冠三載，一被二年。常克儉于身，凡皆此類。五十外便斷房室。”又《資治通鑒》卷一百五十九“梁紀十五”大同十一年條也有類似的記載： “自天監中用釋氏法，長齋斷魚肉。日止一食，惟菜羹糲飯而已。或遇事繁，日移中則嗽口以過。”梁武帝自登基之后，就開始不食葷腥，並堅持“日止一食，過中不食”這一佛教的基本戒律。如果遇到公務繁忙，已經過了正午來不及吃飯，就漱漱口度過這一天。貴為帝王、富有天下的梁武帝如此行事，我們只能將之解釋為他對佛教的極端虔誠。

同樣崇信佛法的宋文帝，有一次“大會沙門，親禦地筵。食至良久，眾疑過中。帝曰：‘始可中耳。’生乃曰：‘白日麗天。天言始中，何得非中。’遂舉箸而食。一眾從之，莫不嘆其機辯。”[4] 這裡的“生”是竺道生，當時的名僧。皇帝請沙門吃飯，廚房動作慢了點，等到飯菜上來，眾沙門懷疑已經過了正午，不敢下筷子。皇帝說：“大概快中午了吧。” 竺道生就說：“太陽依附在天上，天（皇帝）說才剛正午，怎麼會不是呢？”這位竺道生雖然機敏，然而未免有點把佛祖的訓誡當兒戲了。但是這個例子卻揭示出一個問題，也就是說執行“過中不食”這條戒律存在著一定的技術上的難度，因為對這條戒律的正確遵守依賴於對正午時刻的準確測定。

根據《法苑珠林》卷四十二“食時部第五”載：“午時為法，即是食時。過此午時影一發一瞬，即是非時。”[5]由此看來，這“時”與“非時”的分界是非常精確和嚴格的。那麼在沒有鐘錶的古代，人們是如何做到這一點的呢？

從《摩訶僧祇律》卷十七中的一條記載中我們大致可以了解早期佛徒們如何來確定正午時刻：“爾時比丘日暝食，為世人所譏：‘云何沙門釋子夜食？我等在家人尚不夜食，此輩失沙門法，何道之有？’諸比丘聞已，以是因緣往白世尊。佛告諸比丘：‘汝等夜食，正應為世人所嫌，從今日后前半日聽食。當取時，若作腳影，若作刻漏。’”[6]這則記載交代了佛祖教給僧眾的“取時”方法，就是“作腳影”和“作刻漏”。也就是說，在晴好的日子可以通過觀察日影測定正午時刻，在陰雨天可以用刻漏來確定正午時間。這兩種辦法毫無疑問都屬於天文學手段。

二、《時非時經》：一本確定“時食”與“非時食”的技術手冊

在佛藏中，有一部很特別的經典《佛說時非時經》(簡稱《時經》)，全經僅由一份數據表加上少數描述性文字構成。該佛經分別收錄于《高麗大藏經》、《大正新修大藏經》、《中華大藏經》等多種漢文大藏經中，[5]因篇幅不長，又為便於討論，今全文錄之如下：

如是我聞，一時佛住王舍城迦蘭陀竹林園精舍。時佛告諸比丘：“我當為汝說《時非時經》，善思念之。”諸比丘言：“如是世尊，當受教聽。”佛告諸比丘：“是中何者為時？何者為非時？比丘當知：

冬初分，第一十五日七腳為時，四腳半非時，從八月十六日至三十日。第二十五日，八腳為時，六腳八指非時，從九月一日至十五日。第三十五日，九腳為時，七腳六指非時，從九月十六日至三十日。第四十五日，十腳為時，八腳三指非時，從十月一日至十五日。第五十五日，十一腳為時，九腳四指非時[6]，從十月十六日至三十日。第六十五日，十二腳為時，十一腳六指非時，從十一月一日至十五日。第七十五日，十一腳半為時，十腳三指非時[7]，從十一月十六日至三十日。第八十五日，十一腳為時，九腳四指非時，從十二月一日至十五日。

春初分，第一十五日，十腳為時，八腳少三指非時[8]，從十二月十六日至三十日。第二十五日，九腳半為時，七腳少三指非時，從正月一日至十五日。第三十五日，九腳為時，六腳少三指非時，從正月十六日至三十日。第四十五日，八腳為時，五腳少三指非時[9]，從二月一日至十五日。第五十五日，七腳為時，三腳少三指非時，從二月十六日至三十日。第六十五日，六腳為時，三腳少四指非時，從三月一日至十五日。第七十五日，五腳為時，三腳少三指非時，從三月十六日至三十日。第八十五日，四腳為時，二腳少一指非時，從四月一日至十五日。

夏初分，第一十五日，三腳為時，二腳少四指非時，從四月十六日至三十日。第二十五日，二腳為時，一腳少五指非時[10]，從五月一日至十五日。第三十五日，二腳半為時，一腳少三指非時，從五月十六日至三十日。第四十五日，三腳半為時[11]，二腳少二指非時，從六月一日至十五日。第五十五日，四腳半為時，二腳半非時，從六月十六日至三十日。第六十五日，五腳為時，三腳非時[12]，從七月一日至十五日。第七十五日，五腳半為時，三腳半非時[13]，從七月十六日至三十日。第八十五日，六腳為時，四腳半非時[14]，從八月一日至十五日。

如是諸比丘，我已說十二月時非時。為諸聲聞之所應行，憐愍利益故說。我所應作已竟，汝等當行。若樹下空處，露坐思惟，諸比丘莫為放逸，后致悔恨。是我所教戒。”佛說經竟，時諸比丘皆大歡喜，勸助受持。

經文正文到此結束，結尾處又附了偈語一首：“因緣輕慢故，命終墮地獄。因緣修善者，於此生天上。緣斯修善業，離惡得解脫。不善欲因緣，身壞入惡道。”並落款“天竺三藏法師若羅嚴，手執梵本，口自宣譯。涼州道人，于闐城中寫訖。”最后再附偈一首：“披褐懷玉，深智作愚，外如夷人，內懷明珠，千億萬劫，與道同軀。”[7]

從上述經文中，我們可以得知如下與本文有關的四點：

一、《時經》是由一位來自印度的佛教僧人若羅嚴和一名涼州佛教徒在於闐城中合作從梵文譯成漢文，前者口授，后者筆錄。這種佛經的漢譯方式在佛教傳入中土的初期是很常見的。有關若羅嚴事跡的記載很少，據《高麗大藏經·著譯者索引》，若羅嚴西晉（265-316 AD）期間在華活動。

二、《時經》把一年分成冬、春、夏三季，每季分成八個15日。這是具有鮮明印度特色的做法。印度古代一年有三季和六季兩種劃分。三季的劃分又見於《大比丘三千威儀》卷下:“從八月十六日至臘月十五日為一時，百二十日屬冬；以臘月十六日至四月十五日為一時，百二十日屬春；從四月十六日至八月十五日為一時，百二十日屬夏。”[8]半月即15日也是印度古代天文曆法中常用的天文週期，如古代印度把一個朔望月分成兩半，新月到滿月叫白月，滿月到晦叫黑月。

三、《時經》每15日給出兩組數據，一組對應“時”，一組對應“非時”。數據的單位是“腳”，次級單位是“指”。參考其他佛經中類似的數據資料，不難斷定這些數據是關於太陽所投表影長度的週年變化的。如《大方等大集經》卷四十二載：“八月……夜十五時，晝十五時，日午之影長六腳跡。……九月……晝十四時，夜十六時，日午之影長八腳跡。……十月……晝十三時，夜十七時，日午之影長十腳跡。……十一月……晝十二時，夜十八時，日午之影十二腳跡。……十二月…… 晝行十三時，夜行十七時，日轉近北，日午之影十二腳跡。[15]……正月……晝行十四時，夜行十六時，日轉近北，日午之影長八腳跡。……二月……晝行十五時，夜行十五時，日近北行，日午之影長六腳跡。……三月……晝行十六時，夜行十四時，日行近北，日午之影長四腳跡。……四月……晝行十七時，夜行十三時，日近北行，日午之影長兩腳跡。……五月……晝行十八時，夜行十二時，日極行北，日午之影長半腳跡。……六月……晝行十七時，夜行十三時強，日近南行，日午之影長二腳跡。……七月……晝行十六時，夜行十四時，日轉近南，日午之影長四腳跡。”[9]《大集經》中明確表明這些數據是正午的表影長度，所用的單位也是“腳跡”，其中正午影長的週年變化與晝夜長短的週年變化完全吻合。

比較《時經》和《大集經》中的影長變化還可以看出，五月份影長都達到最短，為夏至所在之月；十一月份都達到最長，為冬至所在之月。據此不難推斷《時經》影長資料中二月一日開始的白半月為春分所在位置。春分處在二月的白半月，關於這點其他來自印度的天文資料可作為旁證，如《宿曜經》卷上：“上古白博叉，二月春分朔，於時曜躔婁宿，道齊景正，日中氣和，庶物漸榮，一切增長，梵天歡喜，命為歲元。”[10]又如比《宿曜經》稍早由瞿曇悉達譯出的《九執曆》所載：“九執曆法，梵天所造，五通仙人承習傳授，肇自上古白博叉二月春分朔，於時曜躔婁宿，道曆景止，日中氣和，庶物漸榮，一切增長，動植歡喜，神祗交泰，櫂茲令節，命為歲元。”[11]

四、《時經》把一年當做只有360日。其實從多種漢譯佛經中可以看到印度古代有以30日為一月、12個月為一年的規定。《大比丘三千威儀》中有“百二十日屬冬”、“百二十日屬春”、“百二十日屬夏”的說法，也以360日為一年。又《摩登伽經》卷下載：“三十晝夜名為一月，此十二月名為一歲也。”[12]《舍頭諫太子二十八宿經》載：“三十時名曰須臾，三十須臾為晝夜，三十日為一月，計十二月為一年。”[13]在這兩種佛經中所敘述的也是同樣的規定。《大智度論》卷四十八“釋四念處品第十九”載:“有四種月：一者日月，二者世間月，三者月月，四者星宿月。日月者，三十日半；世間月者，三十日；月月者，二十九日，加六十二分之三十；星宿月者，二十七日，加六十七分之二十一。”[14]這裡所謂的“世間月”正好等於《時經》的兩個半月之和，現在也叫民用月。30民用日為一民用月；12個民用月為一理想年 (ideal year)。這種理想年的概念在古代巴比倫和印度都曾出現過。[15]

經過以上四點的初步分析，可基本斷定：1）《時經》中的這份數據資料中包含著豐富的具有印度淵源的天文和曆法知識；2）這份數據表記錄的是關於表影長度週年變化的資料。然而，與其他佛經資料中給出影長週年變化數據往往只有一套所不同的是，《時經》卻按照“時”和“非時”給出了兩套日影長度值。

關於“時”與“非時”這兩個概念，在佛經中雖然偶有其他含義，但是絕大多數情況下是與“時食”和“非時食”聯繫在一起的。我們知道，對一根規定高度的表，一天中正午的影長最短。《時經》中“時”的影長一律長于對應日子的“非時”的影長，說明“時”所指的時刻還不到正午，應是規定的進食時間；“非時”對應的時刻應該則顯然上午和下午的分界處，也就是正午時刻。

上文提到佛祖教給僧眾的“取時”方法中有“作腳影”一法。這“腳影”一詞正好與《時經》中的影長單位“腳”和《大集經》中的影長單位“腳跡”相互印證。《時經》中的描述，儼然是在為《摩訶僧祇律》中“若作腳影”一語作註腳。結合《時經》開頭的情節描述，我們可以這樣推測：佛祖事先獲得了一年中二十四個半月的正午影長，然后告訴僧眾。僧眾只要在對應的半月里觀察日影的長度，如果日影達到所在半月“時”對應的長度，就可以進食了，若稍稍超過了“非時”對應的長度，這一天就不能再進食了。

至此，我們明白了一份日影長度數據表何以會被當做一部佛經鄭重其事地收入大藏經，因為這部《時非時經》提供了如何斷定正午時刻的“技術參數”，佛徒要根據這一本“技術手冊”來確定進食的時間，做到“時食”而不“非時食”。

三、影長數據處理：“時”與“非時”的進一步解讀

一份完整的影長資料本來應該包含兩個重要的參數：測量影長的表高值H和測量地的緯度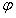，但是這兩個參數《時經》都沒有提供。不過利用一定的球面天文知識和必要的數學手段，不難把這兩個參數解算出來。

先對《時經》中的數據資料稍作整理，可以得到下表1。其中“時”列指“時”所對應的影長數值；“非時”列指“非時”所對應的影長數值，根據上一節的分析，也就是正午時刻的影長。影長單位是“腳”。[16]

表1 《時非時經》中的影長資料

序號	日期	時	非時	序號	日期	時	非時
1	2.1-2.15	8.0	4.7	13	8.1-8.15	6.0	4.5
2	2.16-2.30	7.0	3.7[17]	14	8.16- 8.30	7.0	5.5[18]
3	3.1-3.15	6.0	2.6	15	9.1- 9.15	8.0	6.8
4	3.16-3.30	5.0	2.4[19]	16	9.16-9.30	9.0	7.6
5	4.1-4.15	4.0	1.9	17	10.1-10.15	10.0	8.3
6	4.16-4.30	3.0	1.6	18	10.16-10.30	11.0	9.4
7	5.1-5.15	2.0	0.5	19	11.1-11.15	12.0	10.6[20]
8	5.16-5.30	2.5	1.5[21]	20	11.16-11.30	11.5	10.3
9	6.1-6.15	3.5	1.8	21	12.1-12.15	11.0	9.4
10	6.16-6.30	4.5	2.5	22	12.16-12.30	10.0	7.7
11	7.1-7.15	5.0	3.0	23	1.1-1.15	9.5	6.7
12	7.16-7.30	5.5	3.5	24	1.16-1.30	9.0	5.7

設太陽在正午時刻處於某地（地理緯度為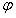）的子午線上，高為H的表所投的日影長度為L，太陽過當地子午圈時的赤緯為d，l為對應的黃經，e為黃赤交角[22]，根據球面天文知識不難得到：

（1）

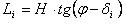
（2）

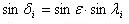
（1）式中表高H和地理緯度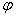是未知數，影長L由表1“非時”列提供，下標i從1變化到24，對應于表1中的序號；太陽黃經λ則相應地從0°開始每隔15°變化到360°，並依次由（2）式給出24個赤緯值δ。[23]（1）式所表示的是一個典型的測量數據處理問題，通過用最小二乘曲線擬合來求解H和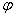，[24]最后得到：

（3）

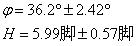
為了檢驗上述求解所得結果的可靠性，可以反過來把（3）式給出的表高和地理緯度值代入（1）式，求出影長（L）的週年變化曲線如下圖1。圖1中的橫坐標是太陽黃經值，縱坐標是影長。圖1中的實線是北緯36.2°處高為5.99腳的表所投射的正午影長週年變化曲線，其中連接叉點的短劃線是表1中“非時”時刻實測影長的週年變化曲線。可見兩者的吻合程度是相當好的，說明前述的求解結果是可靠的。圖1 另附了同一地理緯度處假設表高為6.99腳的理論曲線（點線）和4.99腳表高的理論曲線（點劃線）以供比較。

圖1 北緯36°附近三種不用表高的影長週年變化理論曲線與《時經》實測值的比較

下表2中又給出了根據（3）式的結果計算所得的正午影長理論值（Lc列，單位為腳），以供與《時經》的實測值（Lo列）相比較。表2還列出了從西元元年春分開始的24個定氣公曆日期，以供與《時經》給出的“影長日期”作比較。可以發現，影長的實測值與理論值之間雖然有一定的誤差，但是還是匹配的比較好的。這一點保證了在所求得的地理緯度上，佛徒們根據《時經》提供的這一份影長表能夠很好地避免“非時食”。

表2 《時經》影長實測值及對應日期與理論值的比較

年	月	日	定氣	影長日期	Lo	Lc	年	月	日	定氣	影長日期	Lo	Lc
1	3	23	春分	2.1-2.15	4.7	4.38	1	9	25	秋分	8.1-8.15	4.5	4.38
1	4	7	清明	2.16-2.30	3.7	3.49	1	10	10	寒露	8.16- 8.30	5.5	5.43
1	4	23	穀雨	3.1-3.15	2.6	2.74	1	10	25	霜降	9.1- 9.15	6.8	6.60
1	5	8	立夏	3.16-3.30	2.4	2.14	1	11	9	立冬	9.16-9.30	7.6	7.87
1	5	24	小滿	4.1-4.15	1.9	1.70	1	11	23	小雪	10.1-10.15	8.3	9.07
1	6	9	芒種	4.16-4.30	1.6	1.42	1	12	8	大雪	10.16-10.30	9.4	9.99
1	6	24	夏至	5.1-5.15	0.5	1.33	1	12	23	冬至	11.1-11.15	10.6	10.33
1	7	10	小暑	5.16-5.30	1.5	1.42	2	1	6	小寒	11.16-11.30	10.3	9.99
1	7	26	大暑	6.1-6.15	1.8	1.70	2	1	21	大寒	12.1-12.15	9.4	9.07
1	8	10	立秋	6.16-6.30	2.5	2.14	2	2	5	立春	12.16-12.30	7.7	7.87
1	8	26	處暑	7.1-7.15	3.0	2.74	2	2	20	雨水	1.1-1.15	6.7	6.60
1	9	10	白露	7.16-7.30	3.5	3.49	2	3	7	驚蜇	1.16-1.30	5.7	5.43

以上是對表1中“非時”列數據進行了處理，接下來對 “時”列的數據進行分析。按照佛教戒律，僧侶必須在天明后、正午前的某個時刻進食。《時經》給出了一年中不同季節里“時食”對應的日影長度，此時太陽位於當地子午線以東的某處，它的地平高度τ不難根據“時”的影長和表高由（1）式求得，它偏離子午線的角度即時角t不難根據以下球面天文公式求得：

（4）

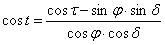
（4）式中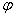是地理緯度，δ是太陽赤緯，由（2）式求出。（4）式求得的是角度，但可以很容易地轉化成小時和分鐘，即距離正午的時間間隔。

如下表3中所示，即使在同一地理緯度，如36°，按照《時經》的“時食”影長算出的“時食”時刻距離正午的間隔也會隨季節發生變化。這一點可作如下解釋：從表1中可以知道，“時食”對應的影長數值大多是整數，只有少數幾個有半腳的值，它們顯示出一種線性變化的趨勢。這顯然不是一組全部靠實測獲得的值，而是有人為規定的成分。從圖1可知，白天某一固定時刻譬如正午的表影長度的週年變化是不均勻的。所以一旦影長變化規定為均勻的，“時食”時刻在午前的位置就不會固定。

表3 不同地理緯度上《時經》“時食”時刻離開正午的時間

節氣

25°

30°

36°

節氣

25°

30°

36°

春分

3^h

14^m

3^h

4^m

2^h

48^m

秋分

2^h

35^m

2^h

21^m

1^h

56^m

清明

3^h

10^m

3^h

4^m

2^h

51^m

寒露

2^h

38^m

2^h

21^m

1^h

51^m

穀雨

3^h

2^m

2^h

57^m

2^h

48^m

霜降

2^h

38^m

2^h

17^m

1^h

40^m

立夏

2^h

47^m

2^h

44^m

2^h

37^m

立冬

2^h

36^m

2^h

12^m

1^h

26^m

小滿

2^h

25^m

2^h

23^m

2^h

16^m

小雪

2^h

35^m

2^h

8^m

1^h

14^m

芒種

1^h

56^m

1^h

54^m

1^h

46^m

大雪

2^h

38^m

2^h

10^m

1^h

14^m

夏至

1^h

20^m

1^h

17^m

1^h

3^m

冬至

2^h

48^m

2^h

21^m

1^h

31^m

小暑

1^h

38^m

1^h

36^m

1^h

25^m

小寒

2^h

45^m

2^h

18^m

1^h

28^m

大暑

2^h

10^m

2^h

7^m

1^h

58^m

大寒

2^h

50^m

2^h

26^m

1^h

43^m

立秋

2^h

34^m

2^h

30^m

2^h

21^m

立春

2^h

52^m

2^h

31^m

1^h

54^m

處暑

2^h

38^m

2^h

32^m

2^h

19^m

雨水

3^h

3^m

2^h

46^m

2^h

18^m

白露

2^h

39^m

2^h

29^m

2^h

11^m

驚蜇

3^h

13^m

3^h

1^m

2^h

40^m

表3還給出了按照《時經》所給出的“時食”影長所指示的“時食”時刻隨地理緯度而變化的情況。平均起來，北緯36°處，“時食”時刻在午前2小時左右；到北緯30°處“時食”平均在午前2小時24分左右；到北緯25°處，“時食”平均在午前2小時37分左右。表3的結果所揭示的《時經》中“時食”的規定與《大方廣佛華嚴經》卷十一中的一條記載也可相互佐證：

仁者當知，居俗日夜，分為八時，于晝與夕，各四時。……我王精勤，不著睡眠。于夜四時，二時安靜。第三時起，正定其心，受用法樂。第四時中，外思庶類，不想貪嗔。自晝初時，先嚼楊枝，乃至祠祭，凡有十位。……日初出時，先召良醫，……次召曆算，……次第二時，進禦王膳。奏妙音樂，種種歡娛，以悅王意。于第三時，沐浴遊宴，……盡第四時，于王正殿，敷置眾寶，莊嚴論座，……[16]

這裡給出了一份佛國君王的作息時間表，在印度古代民用的晝夜八“時”劃分中，晨后午前有兩“時”，王進禦膳的時間正是在午前一“時”，大約在午前2個多小時，符合“時食”的規定。

四、討論和結論

按照《時經》一開頭的描述，該經是佛祖釋迦牟尼住在王舍城[25]迦蘭陀竹林園精舍傳道時向僧眾宣講的，因此其中的影長數據照理應該適用於王舍城所在的地理緯度。王舍城是古印度摩揭陀國都城，在今印度比哈爾（Bihar）邦恒河以南，處於北緯25°左右。但根據本文第三節的計算，《時經》中影長數據的適用地點在北緯36°左右。地理緯度差11°是一個不容忽視的偏差，為了直觀地表示《時經》的影長資料不適合北緯25°處的實際情況，下圖2中繪製了北緯25°處三種表高的正午影長週年變化曲線。其中點劃線、短劃線和點線分別是表高4.99腳、5.99腳和6.99腳的影長變化曲線，實折線是《時經》“非時”數據表示的影長變化。我們看到，不管怎樣調節表高，北緯25°處的影長週年變化曲線與《時經》中的數據都無法吻合。

圖2 北緯25°處三種表高的正午影長週年變化曲線及其與《時經》實測值的比較

因此，本文推斷：《時經》中的“非時”影長數據並不在王舍城測得，即這份《佛說時非時經》中的“非時”影長數據並不出自佛祖之口。從這些數據適用的地理緯度為36.2°±2.42°來看，它們應該在古代印度的西北，即現在的巴基斯坦北部和巴控克什米爾一帶測得，這一帶正是印度佛教文化曾經繁榮的地區。克什米爾在中國古代史書中又稱為罽賓國，是佛教從陸路向中國傳播的始發之地。從罽賓翻越喀拉崑崙山即到達于闐等古代西域諸國，事實上罽賓在中國古代史書中也被看做是西域諸國之一。另外，值得注意的是，《時經》的翻譯地于闐也正在所求得的緯度帶上。

然而，整部《時經》不大可能都是后代佛徒假托佛祖而作。如前節所述，《時經》中的“時食”影長數據明顯出於人為的規定，而這樣的規定由佛祖親自作出是很自然的。按照前文所引《彌沙塞部和醯五分律》卷八中的記載，當時佛祖確實有必要作出這樣的規定。但是，隨著佛教北傳，西北印度、罽賓和西域諸國的信徒，不得不根據當地對正午影長的實測值來對《時經》中的“非時”影長數據進行修改，同時“時食”的數據仍舊保持原樣。所以《時經》中的“時”和“非時”兩套數據反映了佛教從其發源地向西北和古代西域傳播並在該地域停留的情形。

總而言之，《時經》提供的兩套影長數據，為北緯36°附近的佛徒們做到“時食”並避免“非時食”提供了相當可靠的技術保障。同時，這部《時經》還是佛教從其發源地向西北印度和古代西域地區傳播的證據，更是印度天文曆法知識隨佛教向中國傳播的重要證據。

參考文獻：

[1][唐]玄奘譯.阿毗達磨俱舍論.卷14.見：高楠順次郎,等.《大正新修大藏經》.29 冊.東京：大正一切經刊行會.1934.73.

[1]失譯附東晉錄.沙彌十戒法並威儀一卷. 見：高楠順次郎,等.《大正新修大藏經》.24冊.東京：大正一切經刊行會.1934.926.

[1][劉宋]佛陀什，竺道生譯.彌沙塞部和醯五分律.卷8.見：高楠順次郎,等.《大正新修大藏經》.22冊.東京：大正一切經刊行會.1934.54.

[1][宋]志磐.佛祖統紀.卷26.見：高楠順次郎,等.《大正新修大藏經》.49冊.東京：大正一切經刊行會.1934.266.

[1][唐]道世.法苑珠林.卷42.見：高楠順次郎,等.《大正新修大藏經》.53冊.東京：大正一切經刊行會.1934.611.

[1][東晉]佛陀跋陀羅，法顯譯.摩訶僧祇律.卷17.見：高楠順次郎,等.《大正新修大藏經》.22冊.東京：大正一切經刊行會.1934.359.

[1][西晉]若羅嚴譯.佛說時非時經.見：《中華大藏經》編輯局.《中華大藏經》.36冊. 北京：中華書局，1989.367～369.

[1][后漢]安世高譯.大比丘三千威儀.卷下.見：高楠順次郎,等.《大正新修大藏經》.24冊.東京：大正一切經刊行會.1934.925.

[1][隋]那連提耶舍譯.大方等大集經.卷42.見：高楠順次郎,等.《大正新修大藏經》.13冊.東京：大正一切經刊行會.1934.280～282.

[1][唐]不空譯.文殊師利菩薩及諸仙所說吉兇時日善惡宿曜經.卷上.見：高楠順次郎,等. 《大正新修大藏經》.21冊.東京：大正一切經刊行會.1934.388.

[1][唐]瞿曇悉達譯.開元佔經·九執曆.卷104.中國書店，1989。

[1][吳]竺律炎,支謙譯.摩登伽經.卷下.見：高楠順次郎,等.《大正新修大藏經》.21 冊.東京：大正一切經刊行會.1934.409.

[1][西晉]竺法護譯.舍頭諫太子二十八宿經.卷下.見：高楠順次郎,等.《大正新修大藏經》.21冊.東京：大正一切經刊行會.1934.416.

[1][后秦]鳩摩羅什譯.大智度論.卷48.見：高楠順次郎,等.《大正新修大藏經》.25 冊.東京：大正一切經刊行會.1934.409.

[1]Pingree D. History of Mathematical Astronomy in India, in Gillispie C. Ed.: Dictionary of Scientific Biography XVI. New York: Charles Scribners Sons, 1981. 535.

[1][唐]般若譯.大方廣佛華嚴經.卷11.見：高楠順次郎,等.《大正新修大藏經》.10冊.東京：大正一切經刊行會.1934.714.

[1]梵語作Pisaca，一種餓鬼的名稱。

[2]梵語作Payattika，意為“墮”，一種重罪，死后墮入八寒八熱地獄。

[3]指天作白色時，伸手能看見掌文，才可以開始食早粥。

[4]梵語作Duskrta，一種罪名。簫齊僧伽跋陀羅譯《善見律毗婆沙》（《大正藏》第1462號）卷九云：“突吉羅者，不用佛語。突者，惡；吉羅者，作惡、作義也。于比丘行中不善，亦名突吉羅。”

[5]其中《大正藏》和《中華藏》都分別收錄了兩個版本的《時經》，《大正藏》兩個版本共用一個編號，今以794A和794B加以區別；《中華藏》分別編號為H0925和H0926。《大正藏》794A和《中華藏》H0925以《高麗藏》版《時經》（編號為K0857）為底本，但該版本被認為訛誤較多，與其他諸本難以參校，故《大正藏》和《中華藏》以清《乾隆藏》為底本，參校《房山云居寺石經》、宋《資福藏》等諸本，給出了《時經》別本 794B和H0926。作者經過比對，就數據部分而言，794A與794B或者H0925與H0926之間的差異不是很大，但794B和H0926有四個數據給出得比794A和H0925完整。故本文以794B和H0926為基礎。

[6]794A、H0925和《高麗藏》為“九腳三指非時”，《房山云居寺石經》為“九腳非時”。

[7]794A、H0925和《高麗藏》為“十腳一指非時”。

[8]794A、H0925和《高麗藏》為“八腳少一指非時”，《房山云居寺石經》為“八腳三指非時”。

[9]794A、H0925和《高麗藏》為“五腳非時”。

[10]794A、H0925和《高麗藏》為“少三指非時”。

[11]794A、H0925和《高麗藏》為“四腳為時”。

[12]794A、H0925和《高麗藏》為“三腳少非時”。

[13]794A、H0925和《高麗藏》為“三腳少非時”。

[14]794A、H0925和《高麗藏》為“四腳少非時”，《房山云居寺石經》為“四腳非時”。

[15]從影長變化規律來看，此處似應作10腳跡。

[16]《時經》沒有給出1腳等於多少指，但從經文中各數據可以推斷1腳等於10指。

[17]794B、H0926為“三腳少三指非時”，從794B校注、794A、《高麗藏》和《房山云居寺石經》改為“四腳少三指非時”。

[18]794B、H0926為“四腳半非時”，從794A、H0925和《高麗藏》改為“五腳半非時”。

[19]794B、H0926作“三腳少三指非時”，疑有誤。按照影長變化的規律，此處影長應遞減，據794A、H0925和《高麗藏》改為 “三腳少六指非時”。

[20]794B、H0926為“十一腳六指非時”，從794A、H0925和《高麗藏》改為“十腳六指非時”。

[21]794A、H0925和《高麗藏》為“一腳少非時”，從794B校注改為“一腳半非時”。

[22]黃赤交角不是一個常數，由公式ε=84381.448－46.8150T－0.00059T2 + 0.001813T3 決定，單位為角秒，其中T為距離曆元2000.0年的世紀數，曆元以后為正，曆元以前為負。佛滅年代有各種異說，如取前486年說，則前500年佛在世時黃赤交角為23°46′20〃；從下文可知，非時的影長數據極可能是佛滅后若干年的實測結果，本文取西元元年的黃赤交角值23°41′58〃，應不至於有太大誤差。

[23]嚴格來講，一回歸年中每日正午的影長都是不同的，所以本文從24個赤緯值求得的24個影長值只代表24個定氣日的正午影長。然而《時經》每15日只使用一個影長值，這一方面顯然是出於方便的考慮──便於《時經》的規定被執行，但另一方面在精度上就有所欠缺，還使得本文在計算時不得不假定每個影長值對應的日期為各個15日的第一天，實際上也就是定氣日。

[24]本文的計算方法所依據的理論參閱丁月蓉編著的《天文數據處理方法》（南京大學出版社，1998）第二章“誤差概論和最小二乘法”，限于篇幅，此處略去具體計算過程。

[25]王舍城，梵語作Rajagrha，意為國王的住所，為古印度佛教勝地之一，釋迦牟尼早期的傳教中心。音譯為羅閱揭梨醯、羅閱祗、羅閱等，玄奘《大唐西域記》譯作曷羅闍姞利呬城。

來源：“科學視野中的佛教”研討會論文集
http://big5.fjnet.com